예전에 스팀잇이라는 곳에서 포스팅한 내용인데 지금은 활동하지 않아서 티스토리로 옮겨둡니다.
갈릴레이 좌표변환에 대해 저번 시간에 소개했습니다.
운동하는 대상의 관성계와 관측자의 관성계의 관계를 보여주는 관계식이었죠.

그런데 문제가 발생했었습니다.
만약 운동하는 대상인 우주선이 20만km/s로 움직이고 여기서 발사한 로켓이 또 우주선의 진행 방향과 같이 20만km/s라면 갈릴레이 변환에 의해 우리가 관측을 하게 되면 40만km의 로켓이 관측이 됩니다.
갈릴레이 변환이라면 말이죠.

그런데 빛의 속도가 일정하다고 이야기했었습니다.
30만km/s로 일정합니다.
그럼 40만km/s라는 값의 결과가 나오는 갈릴레이변환은 빛의 속도가 일정하다는 사실을 설명해주지 못하기 때문에 우리는 이 값을 설명해주는 좌표변환식을 구해야 합니다.
이 수정한 결과의 좌표변환이 로렌츠 좌표변환이며 지금부터 그 과정을 따라가 보도록 하겠습니다.
좌표변환을 위해 갈릴레이 변환을 우선 써봅시다.

이 변환 행렬에서 우리는 우선 하나의 가정을 합니다.
한 방향으로만 진행한다고 가정합니다.
이렇게 하는 이유는 임의의 방향으로 간다고 가정하면 계산하기에 복잡하고 한 방향으로 간다고 가정하고 구한 다음에 다른 방향까지 고려해도 되기 때문입니다.
그렇기에 하나의 방향인 x방향으로만 진행한다고 가정하고 변환 행렬이 어떻게 될지 구합니다.

그럼 위와 같은 식으로 될 겁니다. (y, z방향으로의 변화는 불변) (알파벳 순으로 a,b,e,d는 미지수 값이며 c가 아닌 e라고 표기한 것은 빛의 속도c와 표기가 헷갈릴 수 있어 e라고 표기합니다.)

왼쪽의 (t,x,y,z)‘의 좌표가 이동하는 계고 오른쪽의 (t,x,y,z)가 정지한 관측자의 계입니다.
(t,x,y,z)’을 A’ (t,x,y,z)을 A계라고 앞으로 표현하겠습니다.
그럼 문제를 풀기위해 필요한 초기조건을 생각해봅시다.
- 우리가 아는 값은 빛의 속도는 불변으로 c(30만km/s)로 일정하다.
- A계의 원점에 고정된 입자(대상)를 A’계에서 관측하면 음의 방향 속도 V로 움직이는 것으로 보일 것이다.(이것은 갈릴레이변환에서도 마찬가지임을 지난 포스팅에서 확인했습니다.)
- A’계의 속도 V가 갈릴레이변환에서 다루는 고전역학의 느린 속도로 근사하면 갈릴레이변환가 일치해야한다. (v=0 => a=1,b=e=0,d=1)
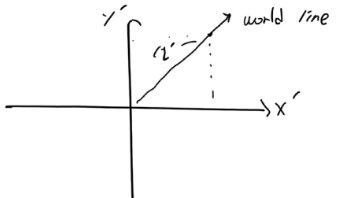
위 초기조건과 가정을 기억하고 저번 포스팅 때 다룬 world line을 다시 보겠습니다.

만약 A계에서의 빛의 World line이 위와 같다고 합시다.
이때 빛의 world line인 ct는 공간상에 퍼져나갑니다. 이 퍼져나가는 것을 x축과 θ(세타)의 각을 이루며 나아가고 이것을 θ(세타)에 대해 x,y로 성분을 분해하여 표시할 수 있습니다.

참고로 위에서 y, z 방향으로는 불변인데 왜 여기서 y방향을 고려하냐는 의문을 가질 수 있습니다. 이 부분은 헷갈리기 쉬운 부분으로 당연히 가질 수 있는 의문입니다.
하지만 명심해야 합니다.
위에서 좌표를 변환한다는 것은 하나의 계(A)에서 다른 계(A’)의 대상을 바라보는 경우 이동하는 대상의 계가 하나의 방향으로 이동한다는 겁니다.
그리고 그 계 안의 운동하는 대상은 어느 방향으로나 이동할 수 있습니다.
다시 말해서 우리가 기찻길에 서서 멀어지고 있는 기차를 보고 있다고 한다면 기차는 일정한 한 방향으로 멀어지지만 그 안에 사람들은 어떠한가요? 앞으로 이동할 수도 있고 뒤로 이동할 수도 있으면 왼쪽 자리에 앉았다가 오른쪽 자리에도 앉을 수 있습니다.
즉, 위에서 x, y방향으로 서술하는 것은 A계에서 바라본 빛이 x, y방향으로 퍼져나가는 world line을 본 것입니다.
그렇기에 하나의 방향으로 이동한다는 말은 관측에 따른 결과로 변환 행렬에 적용하기 위한 가정임을 기억하고 가야 합니다.
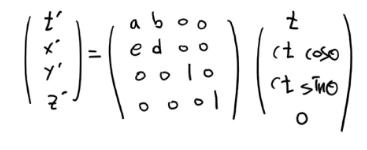
그럼 어느 한 시점의 t시간에서 A계의 좌표값은 (t,ct×cosθ, ct×sinθ)으로 빛의 공간상의 위치를 표현할 수 있습니다.
그렇다면 이때 이 A계에서의 빛을 A’계에서 본다면 다음과 같이 임의의 변환에 의해 A’에서 본 빛을 설명할 수 있습니다.
오른쪽 항을 계산하면 다음과 같습니다.
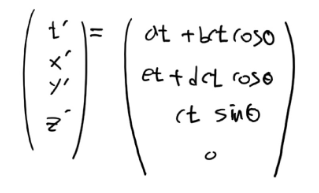
t=0일 때 A계와 A’계의 위치값은 동일하고 t초 후에는 다음과 같이 변할 것을 예측할 수 있습니다.
그렇다면 이 t초후에 A’계에서 바라본 빛의 world line은 다음과 같습니다.
그런데 A’계에서 바라본 ct’도 결국 앞서 본 A계에서의 ct와 같아야 합니다.
ct=ct’이라는 뜻입니다.
왜냐하면 ct라는 값은 속도와 시간의 곱으로 길이의 값입니다. 길이=시간*속도, 60km/h로 1시간을 달린다면 총 60km를 이동하는 것이죠.
그런데 이 이동 거리라는 값은 벡터값이 아닌 스칼라값입니다.
좌표변환을 하였다고 해서 스칼라값은 변하지 않습니다. A계에서 10m 짜리는 결국 A’계에서도 10m이어야 한다는 겁니다.
그래서 이것이 성립하기 위해서는 θ값에 상관없이 피타고라스 정리에 의해 다음의 식을 만족합니다.
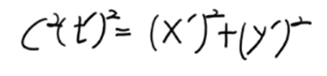
'과학이야기 > 물리 이야기' 카테고리의 다른 글
| 빛의 공간, 4차원 (1) | 2023.02.05 |
|---|---|
| 빛의 속도는 일정하다 (1) | 2023.02.04 |
| 빛의 속도는 항상 일정? (1) | 2023.02.04 |
| 갈릴레이 변환이란? (1) | 2023.02.03 |
| 좌표계란? (1) | 2023.02.03 |