공부하고 정리하고

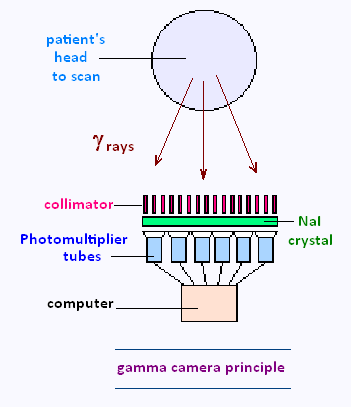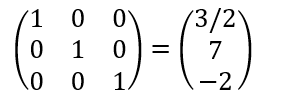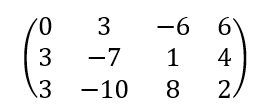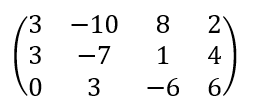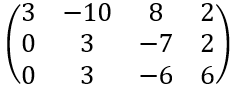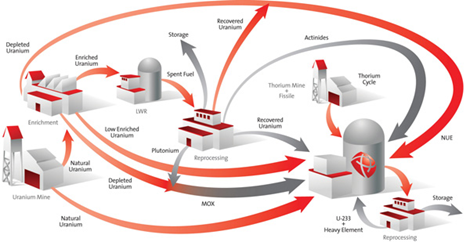
앞으로 원자로 안에서의 핵심구성물인 핵연료집합체에 대해서 먼저 소개하고자 합니다.

핵연료집합체를 기준으로 앞으로 다룰 주 내용입니다.
-핵연료 제작 사이클
-핵연료봉 구조 설명
-독물질봉 구조 설명
-연료집합체로서 구성
-노심에서의 배치

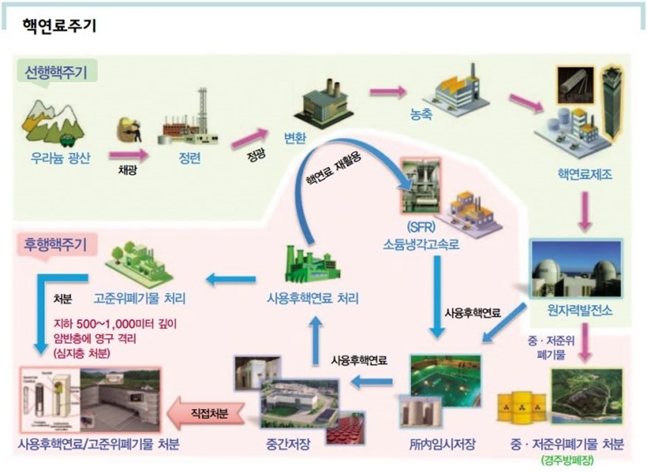
핵연료제작 사이클

핵연료를 제작하고 사용하고 후에 처리하는 과정을 핵연료주기라고 합니다. 이를 사용하는 시점인 원자력발전소에서의 사용을 기준으로 전의 과정을 선행핵연료주기 그 뒤의 과정을 후행핵연료주기라고 합니다.

- 선행핵연료주기

우라늄 원광을 채광하고 정련하고 변환하고 농축하고 가공하는 전 과정을 말합니다.
조금 자세히 알아보겠습니다.

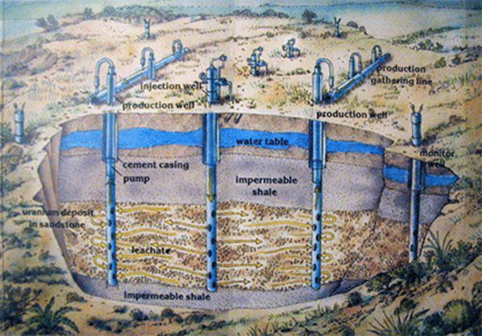
첫 번째 과정인 채광은 우라늄 원광을 채광하는 것을 말합니다. 100m이내의 깊이에 있을 경우는 표토를 제거하고 갱도 없이 바로 채굴하는 방법인 노천채굴을 하고 그 이상일 경우는 갱도채굴을 통해 원광을 채굴합니다.

채굴한 우라늄 원광은 정련이라는 과정을 걸쳐 yellow cake라는 노란색의 우라늄 정광으로 생산됩니다.
방식은 화학적 처리이며 화학을 전공하지 않은 저는 자세히는 모르나 질산에 용해시켜 TBP유기용매로 우라늄을 회수한다고 합니다. 이때 우라늄 정광은 U3O8이라 합니다.

정련의 과정을 거쳐 옐로케이크가 된 우라늄을 변환이라는 과정을 거쳐 중성자 흡수물질과 같은 불순물을 제거하게 됩니다. 이 과정을 통해 옐로케이크는 6불화 우라늄으로 변환됩니다. U3O8 → UF6

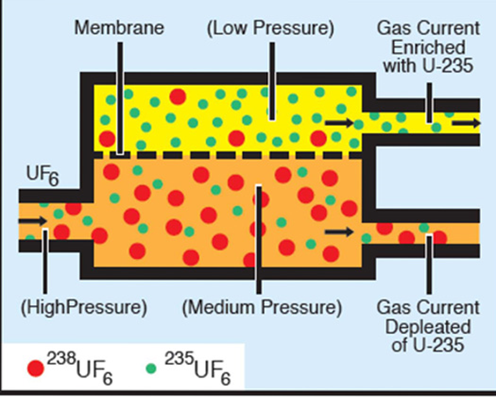
이제 농축의 과정을 지나게 됩니다. 농축은 6불화 우라늄을 기화시켜 기체의 상태로 만들고 기체확산법, 원심분리법, 레이저 농축법 등과 같은 방법으로 농축을 시도합니다.

제가 공부한 교재 기준으로는 기체 확산법 위주로 소개가 되나 과거의 교재이므로 현재 주로 사용하는 농축법은 다른 방법으로 시도가 되고 있을지도 몰라서 이에 대한 소개는 생략하겠습니다. 다만 대부분의 방법이 동위원소 분류법으로 동위원소간의 질량차를 이용한 분리법을 사용한다는 점만 기억하시면 되겠습니다.

기화된 우라늄은 평균 4% 정도의 농축도를 가진 농축 6불화 우라늄으로 농축됩니다. 이때 농축되는 정도는 정확히 몇 %이다가 아니라 여러 농축도를 가진 우라늄을 생산하는데 앞으로 소개되겠지만 원자로 출력안정성 및 효율 증진을 위해 여러 농축 우라늄봉을 사용한다는 점을 기억하시길 바랍니다.

지금까지 따라온 모든 과정은 현재 국내 핵연료 생산 기업인 “한국원자력연료주식회사”에서는 하지 않는 공정입니다. 이 모든 공정은 해외에서 진행이 되며 이 모든 공정이 진행된 농축 6불화 우라늄을 전량 수입하게 됩니다. 앞서 있는 모든 과정을 국내에서 진행하지 않는 이유는 우라늄 원광을 수입하기 때문입니다. 원광으로 수입하면 운송에 부담이 크지만 이렇게 농축까지 진행하여 수입하면 운송에 대한 부담이 줄어들기 때문입니다. 그럼 핵연료주식회사는 어떤 일을 할까요? 이 뒤의 과정인 성형 가공과정을 진행하게 됩니다. 지금부터 설명하는 과정은 국내에서 진행되는 과정입니다.

우선 기체상태의 UF6를 고체상태의 UO2로 변환을 합니다. 산화우라늄으로 만들면 좋은 점은 열에 의한 팽창이 작고 산소와의 반응이 적은 안정성이 있기 때문입니다.
다음으로 고화된 UO2를 균질하게 혼합을 시키고 분말처리 시킵니다.
이제 분말이된 UO2를 하나의 핵연료 펠렛으로 만들기 위한 성형 가공을 합니다.
이 과정은 위아래를 접시 모양으로 들어가도록 모양을 압분의 과정을 거쳐 성형을 하고 약 815도의 고온에서 12시간 정도 소결을 합니다. 이렇게 하면 은회색의 펠렛 세라믹이 만들어집니다.
이렇게 만들어진 펠렛을 연로봉에 장입하여 제작하게 됩니다.
이에 대한 설명은 핵연로봉 구조를 설명할 때 하도록 하겠습니다.
자 이제 핵연로봉은 완성이 되었고 이를 핵연료집합체로 만들어 원자력 발전소로 보내게 됩니다. 이 모든 과정을 선행핵연료주기라고 합니다.

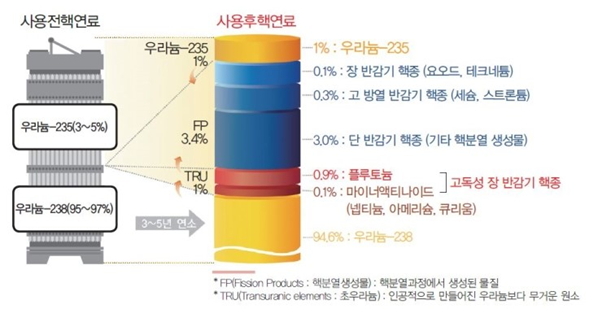
- 후행핵연료주기

원자력발전소는 열심히 전기를 생산하여 이제는 생산효율이 떨어진 핵연료폐기물을 만들어 냅니다. 이 뒤의 과정은 열린 연료주기와 닫힌 연료주기가 있습니다. 현재 우리나라의 분위기는 열린 연료주기일것으로 생각이 되나 아직 법적으로 결정이 되지 않았습니다.

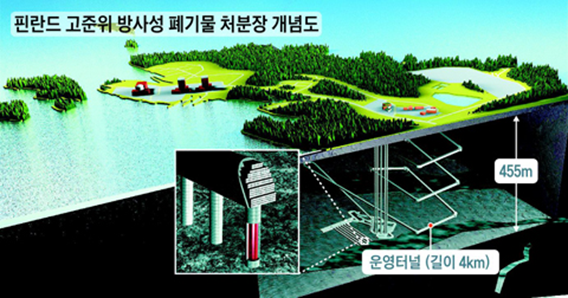
• 열린 연료주기
  여러분들이 흔히 알고 있는 폐기물저장시설에 폐기물을 보관하는 방법입니다. 핵연료폐기물은 폐기물의 방사능에 따라 극저준위, 저준위, 중준위, 고준위로 나눠지는데 핵연료페기물은 고준위에 해당하고 현재 이 고준위폐기물 방폐장은 모든 나라에서 건설에 어려움을 느끼고 있습니다. 누가 자기가 사는 곳에 이 위험하다는 물질을 나두고 싶겠습니까? 아무리 안전하다고 한들 찝찝함이 있음은 사실입니다. 이를 해결하기 위해서는 전문가와 국민들의 소통으로 많은 대화와 지식공유가 오고 가면서 해결되어야 할 문제입니다. 실제 이 고준위 폐기물 보관소를 건설한 필란드의 경우는 국가에 대한 국민들의 신뢰가 높다고 합니다. 그리고 주민들의 걱정을 없애기 위해 실시간으로 소통을 한다고 합니다. 이는 배워야 합니다.

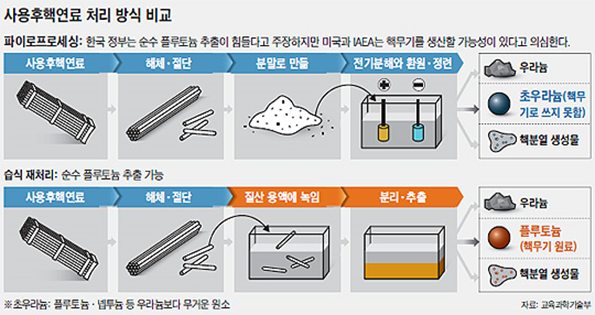
• 닫힌 연료주기
  사용후 핵연료를 재처리하는 방법을 사용하여 다시 사용하는 사이클입니다. 개인적으로는 이 과정이 필요하다고 생각합니다. 왜냐하면 재처리라는 과정을 거치면서 핵연료 폐기물을 많이 줄일 수도 있고 또한 실제 산업이나 연구에 필요한 동위원소를 얻을 수도 있습니다.
  더 나아가 고속증식로가 상업화된다면 이 과정은 필수적으로 필요합니다.

이를 파이로프로세싱이라고 합니다. 하지만 이에 관한 연구는 연구비만 많이 먹은 연구로 낙인이 찍혀있고 실제 원자력연구원쪽에서 이에 관한 연구비가 삭감되고 있다고 합니다. 고속로에 대해서는 나중에 기회가 되면 소개하겠습니다.

하지만 이 과정은 현재 핵무기를 생산할 가능성이 있는 관계로 핵확산방지조약에 가입되어 있는 우리나라는 실시간으로 IAEA(국제원자력기구)로부터 감찰을 받고 있습니다. 그런데 아이러니하게도 평화적으로 사용하겠다고 선언하면 재처리를 하는 것을 허용해주기는 합니다.
그런데 왜 안할까요?....
바로 돈입니다. 이 과정에는 돈이 굉장히 많이 든다고 합니다. 그리고 비싼 돈 들인 것에 비해 재활용되는 비율도 극히 낮습니다.

 오늘은 여기서 포스팅을 마칩니다. 감사합니다!!

 오늘은 방사성동위원소가 진단 분야에서 활용이 되는 PET에 대해서 알아보겠습니다.

양전자란?

양전자라는 말이 익숙하신가요?
제가 예전에 소개했던 반물질에 대해 아시나요? 를 읽어보신 분이라면 익숙하시겠지만 그래도 한 번 더 설명하도록 하겠습니다.

양전자는 흔히 우리가 아는 전자와 부호가 반대인 전자입니다. 그래서 반입자라고도 합니다.
이 반입자는 입자와 만나 소멸하는 반응을 굉장히 잘합니다. 그런데 우리의 우주는 입자와 반입자의 균형이 깨져 입자가 가득한 세상을 이루고 있습니다. 그래서 반입자가 생겨나면 바로 주변의 입자들과 반응하여 소멸하게 됩니다. 이러한 현상은 전자와 양전자 사이에서도 일어납니다.
이를 쌍소멸이라고 하는데 전자와 양전자가 만나서 사라지고 감마선 또는 다른 입자의 형태로 변환됩니다.

이라는 식에 따라서 말입니다.

이때 조건이 있습니다. 이 반응 시 전하량과 운동량, 에너지가 보존이 되어야 합니다.
전하량이 보존이 되기 위해서는 전하량의 합이 0이 되어야 합니다. 그런데 양전자와 전자는 부호만 다르고 양 자체는 같으니까 합하면 0이되어 전하량이 보존이 됩니다.
운동량과 에너지를 보존하기 위해서는 우선 에너지의 경우는 반응 전 후의 에너지 합이 같아야 합니다. 하나의 전자가 가지는 정지질량에 해당하는 에너지는 0.511MeV이고 두 개가 만나 대략 1.1MeV의 에너지가 반응 후의 에너지입니다.
그리고 운동량의 경우는 두개의 입자가 만나서 생기는 결과인 감마선이 반응 전 입자와 운동량 보존을 이루기 위해서는 충돌해서 반응 전 운동량의 합이 0임을 고려해서 반응 후 감마선의 운동량도 0이 되어야 합니다.
이를 위해서는 에너지를 반으로 나눠서 반대 방향으로 방출된다면 운동량의 합을 0으로 만들 수 있습니다.

그래서 결론은 다음과 같습니다.

양전자는 전자와 만나서 쌍소멸을 한다.

쌍소멸시 생성되는 감마선은 두 개로 나뉘어 반대방향으로 방출된다.

자 이제 본론으로 이제 들어가 보겠습니다.

PET?

PET는 Positron Emission Tomography라 하여 양전자 방출 단층 촬영을 말합니다.
양전자를 방출하는 물질을 사용한 단층 촬영법입니다.

그렇다면 왜 양전자를 방출하는 물질을 사용할까요?

양전자는 쌍소멸이라는 반응을 통해 반대 방향으로 나아가는 감마선을 방출하는 특징을 가졌습니다. 즉, 검출기에서 감지가 되었을 때 이 감마선이 어디서 왔는지 역으로 예측이 가능합니다.
위치를 확인할 때 우리는 종양이 있는 곳을 찾아내고 싶습니다. 그래서 이 양전자를 내는 물질을 종양에 보내야 합니다. 종양이 없는 데서 이 양전자를 내고 있으면 PET라는 장비는 무쓸모가 되버리니까요.
그렇다면 한 번 생각해봅시다. 인체 내부에 종양과 같은 것을 찾아내기 위해서 우리가 어떤 방사성동위원소를 사용해야 할까요.? 두가지 정도의 조건이 필요할 것으로 생각이 됩니다.

1. 인체와 거부반응이 없어야 한다.
   거부반응이 없으려면 최대한 화학적 물리적으로 비슷한 물질을 사용해야 합니다. 그래서 우리 몸을 이루고 있는 주요 구성 성분인 산소(O), 질소(N), 탄소(C), 불소(F)의 방사성 동위원소를 활용한다고 합니다.
2. 인체보다는 암과 활발한 반응이 일어나야 한다.
   1번 조건을 통과해서 인체에 들어왔지만 말 그대로 반응이 없이 몸밖으로 배출이 된다면 의미가 없습니다. 그래서 투여되는 방사성 동위원소가 암세포에 모이도록 만들어 줄 필요가 있습니다.

그래서 보통 사용하는게 방사성 의약품인 F-18-불화디옥시포도당이라는 물질이라는데 포도당 유사물질이라고 합니다. 종양이 포도당을 많이 사용하는 특징이 있어 이 물질을 투여하면 종양에 많이 모이게 되고 검출기에서도 이부분이 더 많이 검출되게 됩니다.

영상을 어떻게..?

자 이제 CT에서와 유사합니다. 의료분야에서의 활용2 CT
감마선을 검출하는 검출기가 둘러쌓여있고 이를 검출했을 때 나오는 위치를 데이터화해서 이를 영상화하게 됩니다.
CT와 다른점은 CT는 외부에서 방사선을 조사시켜 감쇠된 정도의 차로 영상을 얻은 반면 PET는 암세포의 존재여부로 영상이 달라지게 됩니다.
그래서 PET의 경우는 암세포와 같은 곳에 모여서 검출되는 특징이 있는것처럼 몸안의 구조를 분별있게 영상화해주지는 못합니다. 이를 보완하기위해 CT의 해부학적 영상을 같이 보도록 보통 PET-CT로 같이 사용하게 됩니다.

PET 말고도 SPECT라는 감마카메라도 존재하는데 양전자를 사용하는 PET과 달리 감마선을 내는 물질을 사용하는 차이가 있지만 영상을 얻어내는 기본적인 원리는 동일한 것으로 알고 있습니다. 그래서 생략하도록 하고 진단 분야에서의 활용은 끝을 맺겠습니다.

오늘은 본격적으로 선형대수학의 첫 번째 주제를 포스팅하도록 하겠습니다.
바로 echelon form에 대한 소개입니다.

Echelon form
간단히 말하자면 Matrix, 행렬의 한 형태입니다. 한글로 번역하면 사다리꼴 행렬이라고 말합니다.
그렇다면 어떤 형태인가?
Matrix가 있으면 한 matrix의 대각선을 기준으로 위쪽에 0이 아닌 값들이 존재하고 그 아래는 모두 0이어서 값이 있는 곳들을 보면 사다리꼴 모양인 matrix를 말합니다.
이 matrix에서의 특징 및 명칭들을 이제 살펴봅시다.

우선 모양을 보면 뒤집혀 있는 사다리꼴 모양입니다.
그리고 ∎표시된 부분은 0이 아닌 값이 열을 기준으로 처음 나오는 값입니다. 그리고 이 ∎를 포함하는 열(column)을 leading entry라고 합니다. *또한 0이 아닌 값입니다.
이 echelon form은 다음과 같은 특징을 가집니다.
(앞으로 행은 row 열은 column이라는 영문표기를 따르겠습니다.)

• row를 기준으로 모든 element가 0인 rowsms 모든 element가 0이 아닌 row보다 아래에 있어야 한다.

그래야 사다리꼴을 보여줄 수 있겠죠?

• 각각의 leading entry들은 위의 row의 leading entry보다 오른쪽에 위치해야 합니다.

이것 또한 사다리꼴이 되려면 필요한 특징입니다.

• 각각의 leading entry column은 ∎아래의 element는 0이어야 한다.

이것 또한 마찬가지 입니다.

여기서 leading entry에서 column의 첫번째 값을 제외하고는 0이 되어야 합니다.
그리고 첫번째 값이 1이 되어야 합니다. 그래야 우리가 해석하기가 쉬워집니다.
이를 위해서 row reduction이라는 과정을 진행해야 합니다. 이를 진행한 echelon matrix를 row reduced echelon matrix라 합니다.

그런데 이를 설명하기에 앞서 연립방정식 한 문제를 풀고 들어가겠습니다.

라는 세 방정식이 있습니다. 이때 a,b,c를 구하라고 하면 어떻게 하면 되죠?
우선 두번째 식에서 첫번째식을 빼보면 2b=14, 즉 b=7이 됩니다. 그리고 a는 3/2가 됩니다. 마지막으로 c는 5-7해서 -2가 됩니다.
이 과정을 행렬로 써볼까요?

마지막으로 해를 구한 값의 행렬로 표현해봅시다.

로 나오게 됩니다. 행렬로 보았을 때 대각선 element를 제외하고는 모두 0입니다.

이 연립방정식을 소개한 이유가 감이 잡히시나요? 우리가 진행할 row reduction이라는 과정은 위 예제와 비슷합니다.
즉, 방법은 간단하게 가장 위의 식인 첫번째 row를 기준으로 하며 그 밑에 식에서 구한 관계들을 대입하여 방정식을 간단하게 표현하게 되는 과정입니다.
이를 위해서 matrix에서는

interchange(0이 아닌 row가 위에 오도록 row 자리 바꿈),

row replacement(특정 값을 곱해 scaling을 해서 0이 되도록 만들기),

scaling(더하고 빼기)의 과정을 통해 계산합니다.

이것도 말로 설명하기보다는 예를 들어서 따라가보겠습니다.

라는 예제가 있을 때 첫번째 row의 첫번째 element가 0입니다. 0이 아닌값이 와야 하니까 interchange를 시켜줍니다.

두번째 row에서 첫번째 row를 빼면 두번째 row의 첫번째 element가 0이 됩니다. 이렇게 하면 첫번째 leading entry가 만족됩니다.

이번에는 세번째 row에서 두번째 row를 빼줍니다. 그럼 두번째 leading entry가 만족됩니다.

여기까지만 진행하면 echelon form이 나오게 됩니다.

그런데 row reduced echelon form을 만들려면 조금 더 계산을 해주어야 합니다. 왜냐하면 leading entry의 element가 1이어야 하기 때문입니다. 이때의 leading entry를 pivot column이라고 하는데 앞으로는 leading entry라는 말보다는 이 pivot column이 계속 나오니까 기억해두면 좋습니다. 그럼 계산을 마저 마무리 지어 보겠습니다.
다음으로 각각의 row의 첫번째 값이 1이 되도록 나눠 주겠습니다.

이 됩니다.

이런 식으로 진행하는 과정이 row reduction입니다. 그리고 이 matrix form은 많은 의미를 담고 있습니다. 그래서 앞으로 소개될 matrix는 이 echelon form이 굉장히 많이 나올 거니까 중요하다는 거 알아주셨으면 좋겠습니다.
오늘은 여기서 포스팅을 마칩니다.