
오늘은 선형대수학에서 사용하는 도구인 행렬에 대해서 알아보고자 합니다. 이 행렬을 알고 있어야 앞으로의 선행대수학에 대한 저의 포스팅에 대해 이해를 하실 수 있습니다. 적분학을 공부하기 위해서 적분기호에 대해 이해를 하고 있어야 하는 것과 마찬가지입니다.
하지만 이 행렬은 수학을 공부 안 하셨다고 하더라도 기본적으로 본 적은 있을 거라고 생각합니다. 만약 본적이 없더라도 아주 쉬운 도구이니까 한 번 같이 알아보겠습니다.
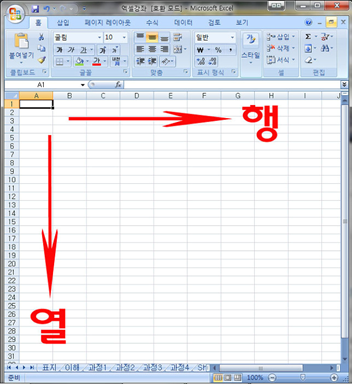
행렬의 행과 렬을 분리해서 생각해보죠.
행은 가로 열은 세로줄입니다.
즉, 가로와 세로줄이라는 뜻이 됩니다. 그래서 가로와 세로로 줄을 세워놓은 수들의 집합입니다.
그래서 아래와 같은 모양으로 표현을 하게 됩니다.

여기서 가로줄이 행 세로줄이 열(렬)이 되는 것입니다. 이 단순한 수의 집합으로 보이는 이 도구는 아주 쉬운 계산 방법을 사용하게 됩니다. 쉽게 말해 더하기, 빼기, 곱하기, 나누기만 할 줄 알면 됩니다.
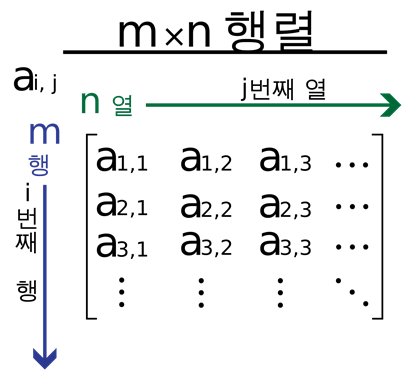
다시 본론으로 돌아오겠습니다. 이 행렬의 각각의 숫자들은 성분이라고 하며 첫 번째 행 첫 번째 열 숫자를 1행 1열의 성분이라고 합니다. 이런식으로 각각의 성분들에게 자리를 매기게 됩니다.
그리고 몇 행 몇 열이냐에 따라 m개의 행과 n개의 열이 있다면 m×n 행렬이라고 말할 수 있습니다.
정리하자면 행과 열의 집합이고 각각의 수들은 몇행, 몇열로 몇번째 자리에 있다라고 말할 수 있는 성분들의 집합이 행렬이라고 할 수 있습니다.
이 행렬이 중요한 이유는 수학을 해석할 때 사용할 수 있기 때문입니다.
방정식 문제를 풀 때 사용이 가능하죠.
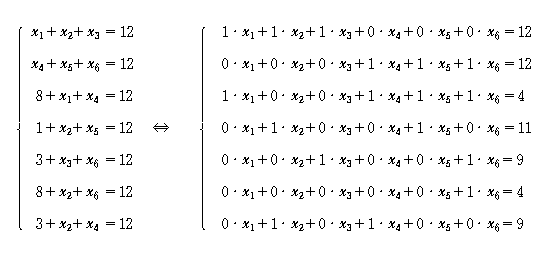
위와 같은 연립 방정식이 있을 때 각각의 변수들 앞에 계수(숫자)들은 행렬의 성분들이고 변수의 개수가 열의 개수이고 방정식의 수가 행의 수가 됩니다.
이렇게 연립방정식을 푸는데 사용할 수 있기 때문에 행렬의 계산 방법을 적용해 문제를 풀 수 있게 됩니다. 그렇기 때문에 쉽게 다가갈 수 있는 것이고 앞으로도 우리는 이런 연립방정식을 푸는 방법에 대해 보게 될 겁니다.
다음 시간에는 간략하게 행렬의 계산 방법에 대해 소개하도록 하겠습니다.
“해당 포스팅에 사용한 이미지는 구글 이미지임을 알립니다.”
“해당 포스팅은 스팀잇에서 작성한 글을 옮긴 포스팅입니다.”
'과학이야기 > 선형대수학' 카테고리의 다른 글
| echelon form (0) | 2018.07.15 |
|---|---|
| 행렬 계산방법 (0) | 2018.06.28 |
| 벡터와 스칼라 (0) | 2018.06.17 |