이 세상은 무엇으로 이루어져 있을까?
우리가 사는 세상은 입자의 세상입니다.
크게 페르미-디락 통계를 따르는 입자와 보스-아인슈타인 통계를 따르는 입자로 나눌 수 있습니다.

페르미-디락통계를 따르는 입자는 같은 상태로 존재하지 않는 입자를 말합니다. 파울리 배타원리를 따르는 입자라고도 합니다.
같은 상태로 존재하지 않는다는 것은 다른 특징을 가졌다고 볼 수 있습니다.
두 사람을 보고 비교할 때 키, 몸무게, 성별, 얼굴 등으로 두 사람을 비교할 수 있습니다. 절대 완전히 똑같은 사람은 없습니다.
이처럼 상태가 다른 입자들을 같은 상태로 존재하지 않는다고 할 수 있습니다.
양자역학에서는 이것을 양자수가 다르다고 말합니다.
이 양자수는 주양자수, 궤도양자수, 자기양자수, 스핀양자수가 있습니다.
각각의 개념을 다 설명하기에는 글이 길어집니다.
그냥 상태를 구별하는 특징이라고만 이해하고 넘어가도록 하겠습니다.
여기서 모든 양자수가 같은 상태라면 구별하기 위해서는 스핀양자수만큼은 달라야 합니다.
이런 표현을 사용해도 되는지 모르겠지만 주양자수에서 자기양자수까지의 양자수 상태는 구별하기 쉬운 특징이라고 보면 됩니다. 얼굴, 키, 체형 등입니다.
그럼 겉으로 구별하기 어려운 일란성쌍둥이가 있는데 완전 똑같이 생겨 구별할 수 없다고 하겠습니다. 이 경우는 겉으로 봐서는 구별하기 힘듭니다.
그런데 한 명은 점이 있고 한 명은 점이 없다고 하면 이것으로 구별을 지을 수도 있겠죠.
제대로 된 예시는 아니지만 페르미-디락 통계에 따르는 입자는 다른 양자수가 같다면 스핀양자수가 달라야 합니다.
이 페르미-디락 통계를 따르는 입자를 페르미입자라고 하며 우리가 아는 거의 모든 입자가 이 페르미입자입니다.
페르미입자는 반정수의 스핀양자수를 가지며 가장 기본입자인 쿼크와 렙톤이 이 페르미입자입니다.
한편, 보스-아인슈타인 통계는 열적 평형상태에서 식별 불가능한 보스 입자의 통계적 분포를 결정하는 통계입니다.
즉, 보스-아안슈타인 통계를 따르는 입자는 입자를 구별할 수 없는 상태입니다.
즉, 여러 입자가 동일한 상태에 있다는 것을 알 수 있습니다.
그렇기에 이 통계를 따르는 입자인 보손은 정수배의 스핀양자수를 가집니다.
광자의 경우에는 1, 힉스의 경우 0의 스핀양자수를 가집니다.
이 보손입자에는 광자, 글루온, W,Z 보손, 힉스 보손이 있습니다.
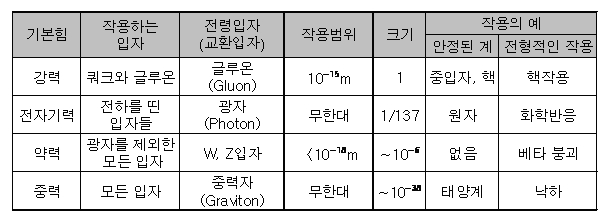
즉, 힘을 매개하는 입자 그리고 질량을 매개하는 입자입니다.
또한 페르미입자는 쿼크와 렙톤으로 양성자, 중성자, 전자가 페르미입자임을 알 수 있습니다.
'과학이야기 > 물리 이야기' 카테고리의 다른 글
| 좌표계란? (1) | 2023.02.03 |
|---|---|
| 특수상대론과 일반상대론 (1) | 2023.02.03 |
| 맥스웰 방정식에 대해 (0) | 2018.11.08 |
| 입자의 위치에 대한 논쟁 3가지 주장들 (0) | 2018.11.07 |
| 정전기를 이용한 가속장치 (0) | 2018.10.25 |