공부하고 정리하고

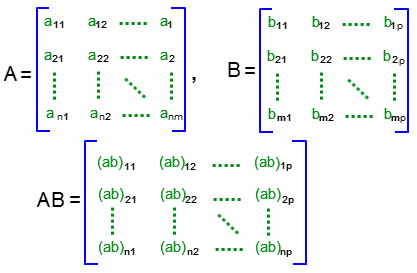
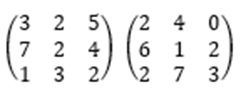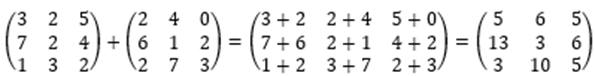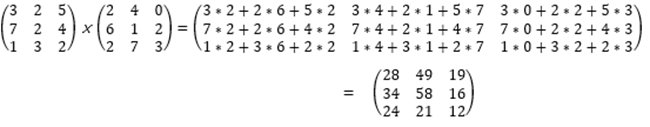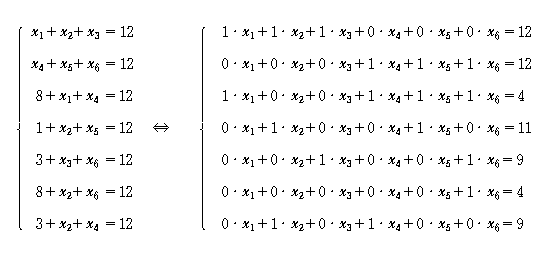오늘은 본격적으로 선형대수학의 첫 번째 주제를 포스팅하도록 하겠습니다.
바로 echelon form에 대한 소개입니다.

Echelon form
간단히 말하자면 Matrix, 행렬의 한 형태입니다. 한글로 번역하면 사다리꼴 행렬이라고 말합니다.
그렇다면 어떤 형태인가?
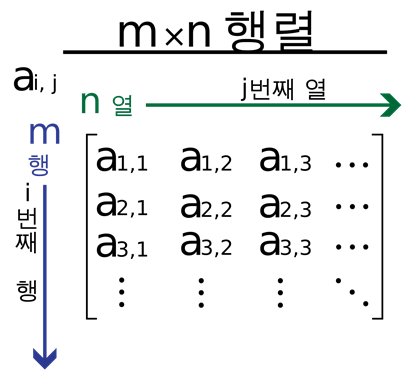
Matrix가 있으면 한 matrix의 대각선을 기준으로 위쪽에 0이 아닌 값들이 존재하고 그 아래는 모두 0이어서 값이 있는 곳들을 보면 사다리꼴 모양인 matrix를 말합니다.
이 matrix에서의 특징 및 명칭들을 이제 살펴봅시다.

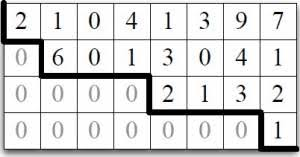
우선 모양을 보면 뒤집혀 있는 사다리꼴 모양입니다.
그리고 ∎표시된 부분은 0이 아닌 값이 열을 기준으로 처음 나오는 값입니다. 그리고 이 ∎를 포함하는 열(column)을 leading entry라고 합니다. *또한 0이 아닌 값입니다.
이 echelon form은 다음과 같은 특징을 가집니다.
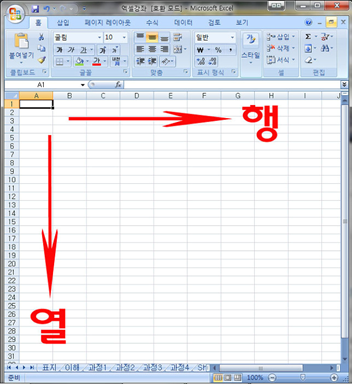
(앞으로 행은 row 열은 column이라는 영문표기를 따르겠습니다.)

• row를 기준으로 모든 element가 0인 rowsms 모든 element가 0이 아닌 row보다 아래에 있어야 한다.

그래야 사다리꼴을 보여줄 수 있겠죠?

• 각각의 leading entry들은 위의 row의 leading entry보다 오른쪽에 위치해야 합니다.

이것 또한 사다리꼴이 되려면 필요한 특징입니다.

• 각각의 leading entry column은 ∎아래의 element는 0이어야 한다.

이것 또한 마찬가지 입니다.

여기서 leading entry에서 column의 첫번째 값을 제외하고는 0이 되어야 합니다.
그리고 첫번째 값이 1이 되어야 합니다. 그래야 우리가 해석하기가 쉬워집니다.
이를 위해서 row reduction이라는 과정을 진행해야 합니다. 이를 진행한 echelon matrix를 row reduced echelon matrix라 합니다.

그런데 이를 설명하기에 앞서 연립방정식 한 문제를 풀고 들어가겠습니다.

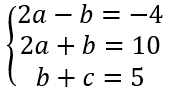
라는 세 방정식이 있습니다. 이때 a,b,c를 구하라고 하면 어떻게 하면 되죠?
우선 두번째 식에서 첫번째식을 빼보면 2b=14, 즉 b=7이 됩니다. 그리고 a는 3/2가 됩니다. 마지막으로 c는 5-7해서 -2가 됩니다.
이 과정을 행렬로 써볼까요?

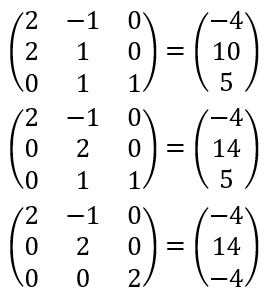
마지막으로 해를 구한 값의 행렬로 표현해봅시다.

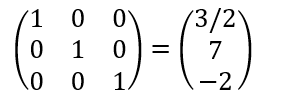
로 나오게 됩니다. 행렬로 보았을 때 대각선 element를 제외하고는 모두 0입니다.

이 연립방정식을 소개한 이유가 감이 잡히시나요? 우리가 진행할 row reduction이라는 과정은 위 예제와 비슷합니다.
즉, 방법은 간단하게 가장 위의 식인 첫번째 row를 기준으로 하며 그 밑에 식에서 구한 관계들을 대입하여 방정식을 간단하게 표현하게 되는 과정입니다.
이를 위해서 matrix에서는

interchange(0이 아닌 row가 위에 오도록 row 자리 바꿈),

row replacement(특정 값을 곱해 scaling을 해서 0이 되도록 만들기),

scaling(더하고 빼기)의 과정을 통해 계산합니다.

이것도 말로 설명하기보다는 예를 들어서 따라가보겠습니다.

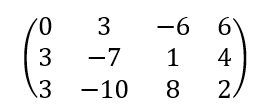
라는 예제가 있을 때 첫번째 row의 첫번째 element가 0입니다. 0이 아닌값이 와야 하니까 interchange를 시켜줍니다.

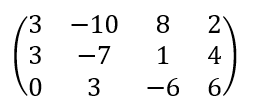
두번째 row에서 첫번째 row를 빼면 두번째 row의 첫번째 element가 0이 됩니다. 이렇게 하면 첫번째 leading entry가 만족됩니다.

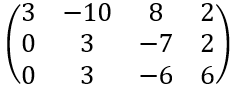
이번에는 세번째 row에서 두번째 row를 빼줍니다. 그럼 두번째 leading entry가 만족됩니다.

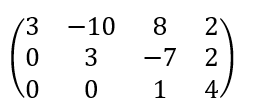
여기까지만 진행하면 echelon form이 나오게 됩니다.

그런데 row reduced echelon form을 만들려면 조금 더 계산을 해주어야 합니다. 왜냐하면 leading entry의 element가 1이어야 하기 때문입니다. 이때의 leading entry를 pivot column이라고 하는데 앞으로는 leading entry라는 말보다는 이 pivot column이 계속 나오니까 기억해두면 좋습니다. 그럼 계산을 마저 마무리 지어 보겠습니다.
다음으로 각각의 row의 첫번째 값이 1이 되도록 나눠 주겠습니다.

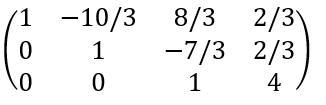
이 됩니다.

이런 식으로 진행하는 과정이 row reduction입니다. 그리고 이 matrix form은 많은 의미를 담고 있습니다. 그래서 앞으로 소개될 matrix는 이 echelon form이 굉장히 많이 나올 거니까 중요하다는 거 알아주셨으면 좋겠습니다.
오늘은 여기서 포스팅을 마칩니다. 

이번 시간에는 행렬의 사칙연산을 어떻게 하는지 알아보겠습니다.

두 개의 행렬을 준비합시다. 행이 3개고 열이 3개인 3ⅹ3행렬 두개를 예로 들겠습니다.

두 행렬을 보겠습니다.
더하기는 매우 간단합니다. 각각의 원소들은 몇행 몇열로 자리를 표현할 수 있다고 했었습니다. 그래서 더하기에서는 이 같은 자릿값끼리 더해주면 됩니다. 아래와 같이 말이죠.

빼기도 같은 방법으로 진행이 됩니다.

곱하기는 조금 다른 방법으로 진행이 됩니다.
3ⅹ3행렬과 3ⅹ3행렬을 곱하면 3ⅹ3행렬의 답이 나오지만
2ⅹ3행렬과 3ⅹ2행렬을 곱하면 2ⅹ2행렬이 나옵니다.
이게 무슨 말인가 하면 앞의 행렬의 행과 뒤의 행렬의 열 개수만큼 답이 나온다는 말입니다.
즉, mⅹn행렬과 nⅹp행렬의 곱은 mⅹp 행렬로 나오게 됩니다.
왜이렇게 되는지 예제로 한번 알아보겠습니다.
앞서 사용한 예제를 한 번 더 사용하겠습니다.

어떻게 계산하는지 아시겠나요?
첫 번째 행렬의 행과 두 번째 행렬의 열을 곱해서 더해주는 값이 각각의 원소들의 결과값입니다.
그렇기에 결과 값이 앞의 행렬의 행개수와 뒤 행렬의 열개수로 결정이 되어지게 됩니다.

그리고 다음으로 행렬의 나눗셈에 해당하는 역행렬을 알아보죠.
역행렬과 행렬을 곱하면 단위행렬이 나옵니다. 이 단위행렬은 대각선 방향값이 1이고 나머지가 모두 0인 일반 산수에서 1에 해당하는 값입니다.

이 역행렬은 고등학교 때까지 2ⅹ2 행렬로 바꾸는 방법을 공식으로 외워왔습니다.

로 말입니다. 그런데 앞으로 역행렬을 구할 때 2ⅹ2 이상에서도 구해야할 경우가 있습니다.
이때 푸는 방법은 고차원 행렬에서 partitioned matrix인 블록으로 나누어 위 2ⅹ2 행렬로 구하는 방법도 있지만 이는 계산이 복잡하고 개인적으로는 echelon matrix로 구하는 방법이 가장 쉬운 방법입니다. 이부분은 나중에 더 자세히 다루겠습니다.

마지막으로 전치행렬에 대해서 알아보겠습니다.
전치행렬은 행과 열을 바꾸는 행렬을 말합니다.
이것도 예를 들어보죠.

와 같은 방법입니다. 3x2가 2x3이 되면서 행과 열이 자리가 바뀌었습니다.

(2,1)이 (1,2)로 (3,1)이 (1,3)의 자리로 옮기며 (1,1), (2,2), (3,3)와 같은 대각선 자리의 숫자는 그대로임을 볼 수 있습니다.  

“해당 포스팅에 사용한 이미지는 구글 이미지임을 알립니다.”

“해당 포스팅은 스팀잇에서 작성한 글을 옮긴 포스팅입니다.”

오늘은 선형대수학에서 사용하는 도구인 행렬에 대해서 알아보고자 합니다. 이 행렬을 알고 있어야 앞으로의 선행대수학에 대한 저의 포스팅에 대해 이해를 하실 수 있습니다. 적분학을 공부하기 위해서 적분기호에 대해 이해를 하고 있어야 하는 것과 마찬가지입니다.

하지만 이 행렬은 수학을 공부 안 하셨다고 하더라도 기본적으로 본 적은 있을 거라고 생각합니다. 만약 본적이 없더라도 아주 쉬운 도구이니까 한 번 같이 알아보겠습니다.

행렬의 행과 렬을 분리해서 생각해보죠.
행은 가로 열은 세로줄입니다.
즉, 가로와 세로줄이라는 뜻이 됩니다. 그래서 가로와 세로로 줄을 세워놓은 수들의 집합입니다.
그래서 아래와 같은 모양으로 표현을 하게 됩니다.

여기서 가로줄이 행 세로줄이 열(렬)이 되는 것입니다. 이 단순한 수의 집합으로 보이는 이 도구는 아주 쉬운 계산 방법을 사용하게 됩니다. 쉽게 말해 더하기, 빼기, 곱하기, 나누기만 할 줄 알면 됩니다.

다시 본론으로 돌아오겠습니다. 이 행렬의 각각의 숫자들은 성분이라고 하며 첫 번째 행 첫 번째 열 숫자를 1행 1열의 성분이라고 합니다. 이런식으로 각각의 성분들에게 자리를 매기게 됩니다.
그리고 몇 행 몇 열이냐에 따라 m개의 행과 n개의 열이 있다면 m×n 행렬이라고 말할 수 있습니다.
정리하자면 행과 열의 집합이고 각각의 수들은 몇행, 몇열로 몇번째 자리에 있다라고 말할 수 있는 성분들의 집합이 행렬이라고 할 수 있습니다.
이 행렬이 중요한 이유는 수학을 해석할 때 사용할 수 있기 때문입니다.
방정식 문제를 풀 때 사용이 가능하죠.

위와 같은 연립 방정식이 있을 때 각각의 변수들 앞에 계수(숫자)들은 행렬의 성분들이고 변수의 개수가 열의 개수이고 방정식의 수가 행의 수가 됩니다.
이렇게 연립방정식을 푸는데 사용할 수 있기 때문에 행렬의 계산 방법을 적용해 문제를 풀 수 있게 됩니다. 그렇기 때문에 쉽게 다가갈 수 있는 것이고 앞으로도 우리는 이런 연립방정식을 푸는 방법에 대해 보게 될 겁니다.

다음 시간에는 간략하게 행렬의 계산 방법에 대해 소개하도록 하겠습니다.

“해당 포스팅에 사용한 이미지는 구글 이미지임을 알립니다.”

“해당 포스팅은 스팀잇에서 작성한 글을 옮긴 포스팅입니다.”