오늘은 가장 기본이 되는 개념인 벡터에 대해서 알아보려고 합니다.
이 벡터에 대한 개념은 아마도 중학교? 때 처음 배웠던 것으로 기억을 하는데요.
상당히 중요한 개념이고 물리학을 다루는 데 있어 매우 중요하죠.
그리고 선형대수학을 다루면서 벡터라는 글씨는 지겹게 볼 수 있습니다. 그렇기에 벡터에 대해 처음 들어보시는 분들을 위해서 오늘은 벡터와 스칼라를 알아보고 가겠습니다.

스칼라
스칼라는 크기입니다. 사과 1개, 사람 1명, 속력 ~얼마와 같은 값들이죠. 즉, 방향성이 없는 그저 크기를 나타내는 값들을 스칼라라고 합니다.
그렇기에 좌표계가 변해도 변하지 않는 값을 가지게 됩니다.
이 말은 선형대수학 포스팅을 듣다 보면 조금 더 자세히 이해가 될 겁니다.
벡터
벡터는 방향성이 있는 값을 말합니다.
북쪽으로 1m를 갔다. 북쪽으로 10m/s로 이동했다.
이처럼 크기와 더불어 방향이 같이 제시되는 값들을 말합니다.
스칼라와 벡터를 비교하는 가장 쉬운 방법은 이동거리와 변위로 설명이 됩니다.
이동거리는 스칼라값이고 변위는 벡터값인데 이를 하나의 예로 명확히 이해가 갈 겁니다.
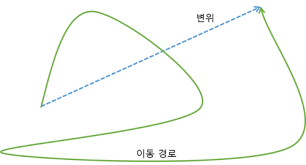
<예시>
겨울이 된 요즘 살이 찐 저는 1000m 걷기를 하기로 했습니다.
그래서 운동장으로 갔습니다. 그리고 만보기 어플을 깔아서 작동을 시켰습니다. 운동장 둘레가 200m였는데 5바퀴를 돌면 목표 달성이겠군요. 그렇게 생각하고 저는 5바퀴를 열심히 돌았습니다. 다 돌고 나니 힘들군요. 그리고 만보기 어플을 킵니다. 그런데 기록은 0m입니다. 어라? 왜 이러는 거지 난 1000m를 돌았는데 이 어플은 0m라는군요. 무슨 일일까요?
실제로는 이렇게 만들지는 않지만 이 어플은 여기서 변위를 적용했습니다. 이동거리가 아니라요.
변위는 시작점으로부터 종점까지의 최단거리를 말합니다. 여기서 최단거리라는 말은 시작점에서 종점까지를 직선으로 그어서 가는 방향이 존재하게 됩니다. 그런점에서 같은곳에서 출발해 1000m를 돌고 다시 원점으로 돌아온 저에게는 변위는 0이 되는 것이지요. 즉, 변한 정도가 0이라는 말입니다.
반면에 스칼라값인 이동거리는 어떤가요? 이동거리는 시작점에서 얼마나 변했는지는 관심이 없습니다. 그저 얼마나 걸었는지가 궁금한 것이고 그 이동한 궤적에 따라 이동한 거리를 다 세는 것입니다. 즉, 방향에는 관심이 없는 값이죠.
이와 비슷하게 속도와 속력의 개념도 벡터와 스칼라의 개념으로 나뉘죠.

벡터가 중요한 이유?
사실, 스칼라 개념이 일상적으로 보았을 때는 더 중요한 값으로 생각이 되어지나 벡터값은 상당한 의미가 있습니다.
물리학이나 공학이나 다른 학문도 마찬가지이지만 우리는 어떠한 일이든 효율을 향상시키기 위해서 노력합니다. 심지어 자연계도 이 효율이 높은 방향으로 모든 운동을 하게 됩니다. 그런 의미에서 벡터를 이해한다는 것은 어떤 방법이 효율이 높은 방향인지를 이해하게 해주는 좋은 도구가 됩니다.
다음 시간에는 선형대수학의 도구인 행렬에 대해서 알아보겠습니다.
“해당 포스팅에 사용한 이미지는 구글 이미지임을 알립니다.”
“해당 포스팅은 스팀잇에서 작성한 글을 옮긴 포스팅입니다.”
'과학이야기 > 선형대수학' 카테고리의 다른 글
| echelon form (0) | 2018.07.15 |
|---|---|
| 행렬 계산방법 (0) | 2018.06.28 |
| 행렬이란? (0) | 2018.06.17 |